Introduction to fitur

Basic Function

fitur is a package to provide wrapper functions for fitting univariate distributions. The main function is fit_univariate where you can supply numeric data to the function along with the desired attributes of the distribution you want to fit. It returns a list object with the density, distribution, quantile, and random deviates functions based on the calculated parameters from the given numeric vector. The parameter estimation is done with MLE.

Discrete Distributions

set.seed(42)
x <- rpois(1000, 3)
fitted <- fit_univariate(x, 'pois', type = 'discrete')
# density function
plot(fitted$dpois(x=0:10),
     xlab = 'x',
     ylab = 'dpois')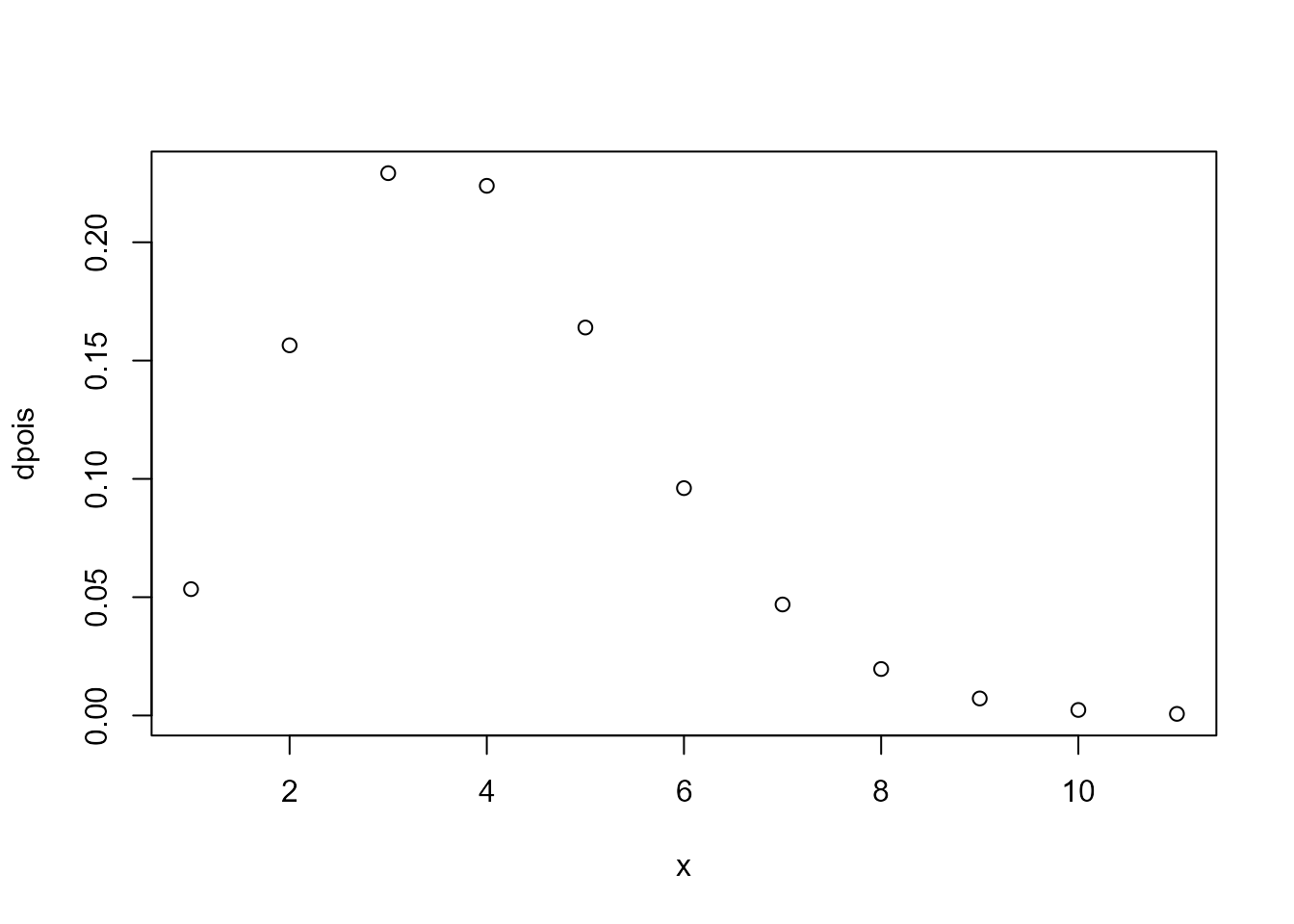

# distribution function
plot(fitted$ppois(seq(0, 10, 1)),
     xlab= 'x',
     ylab = 'ppois')

# quantile function
plot(fitted$qpois,
     xlab= 'x',
     ylab = 'qpois')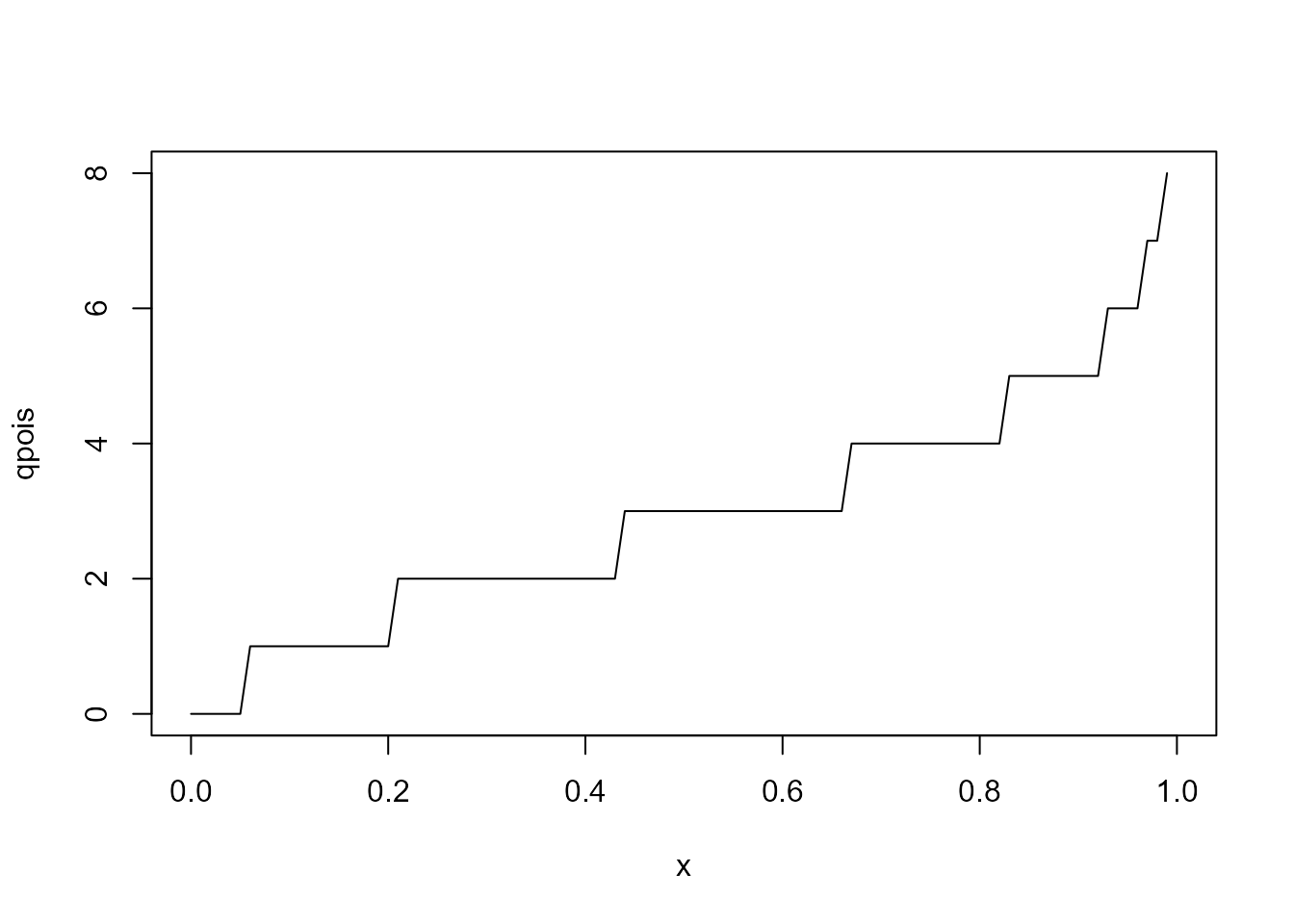

# sample from theoretical distribution
summary(fitted$rpois(100))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    0.00    1.00    3.00    2.75    4.00   10.00

# estimated parameters from MLE
fitted$parameters

## lambda 
##   2.93

Continuous Distributions

set.seed(24)
x <- rweibull(1000, shape = .5, scale = 2)
fitted <- fit_univariate(x, 'weibull')
# density function
plot(fitted$dweibull,
     xlab = 'x',
     ylab = 'dweibull')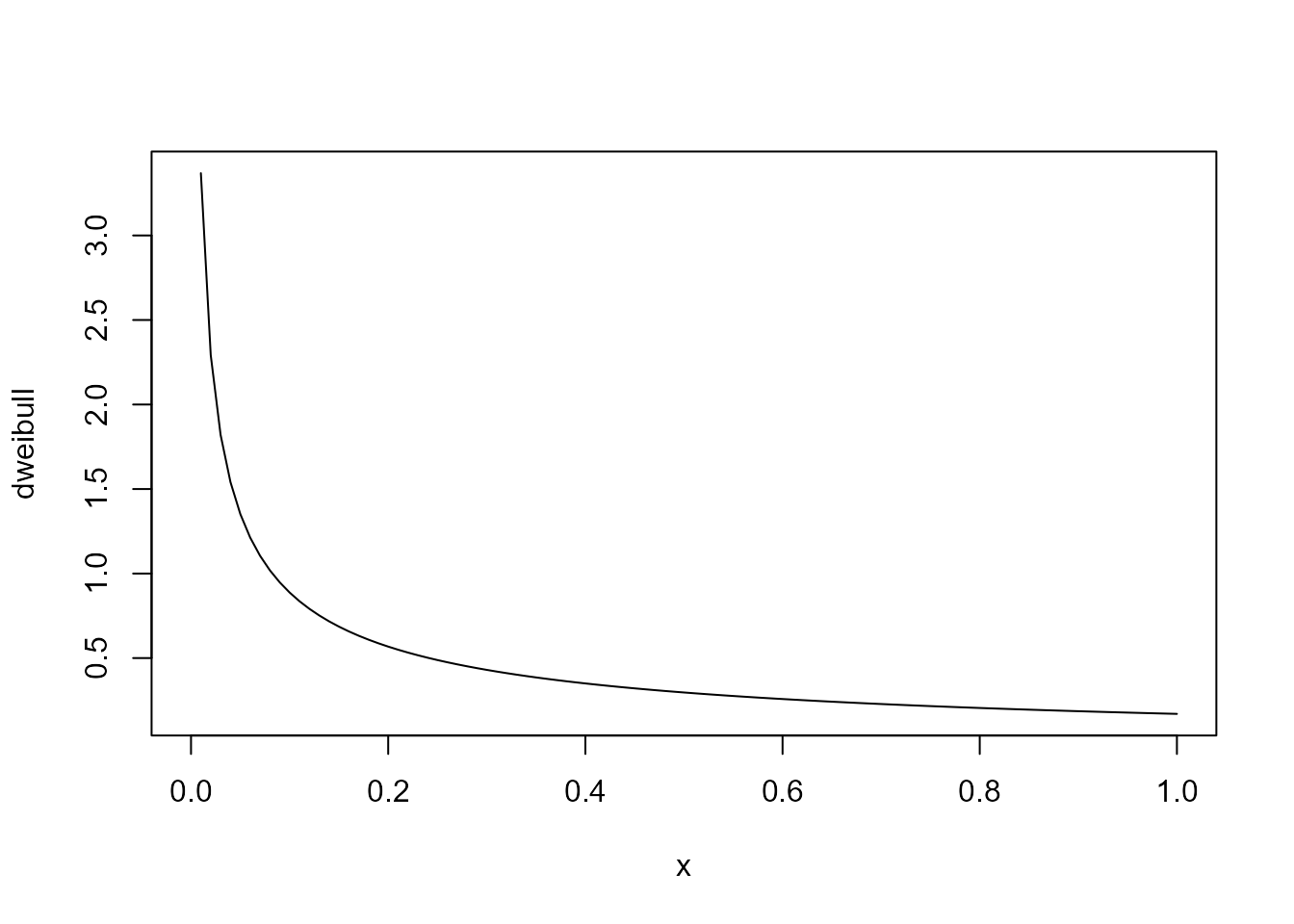

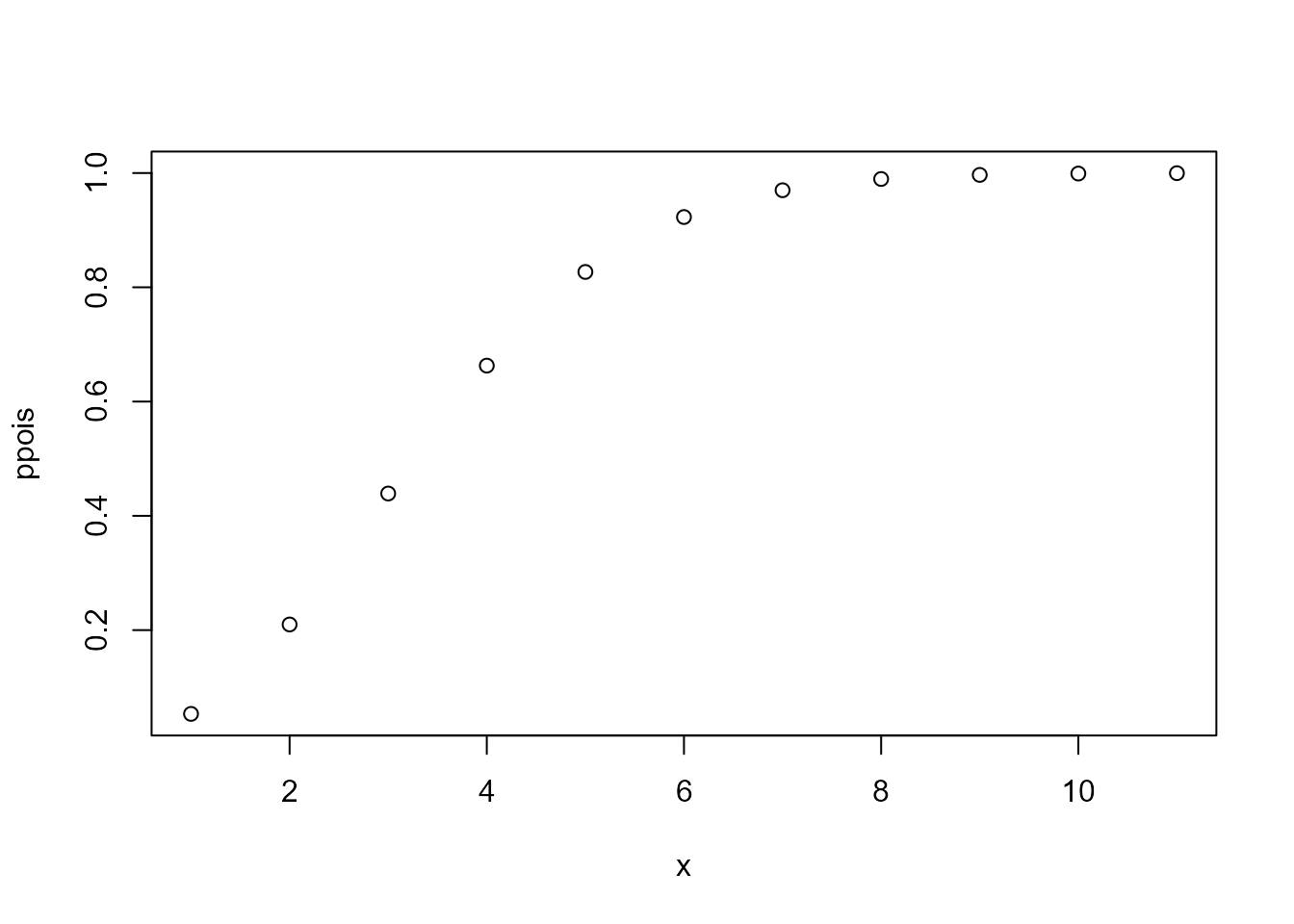
# distribution function
plot(fitted$pweibull,
     xlab = 'x',
     ylab = 'pweibull')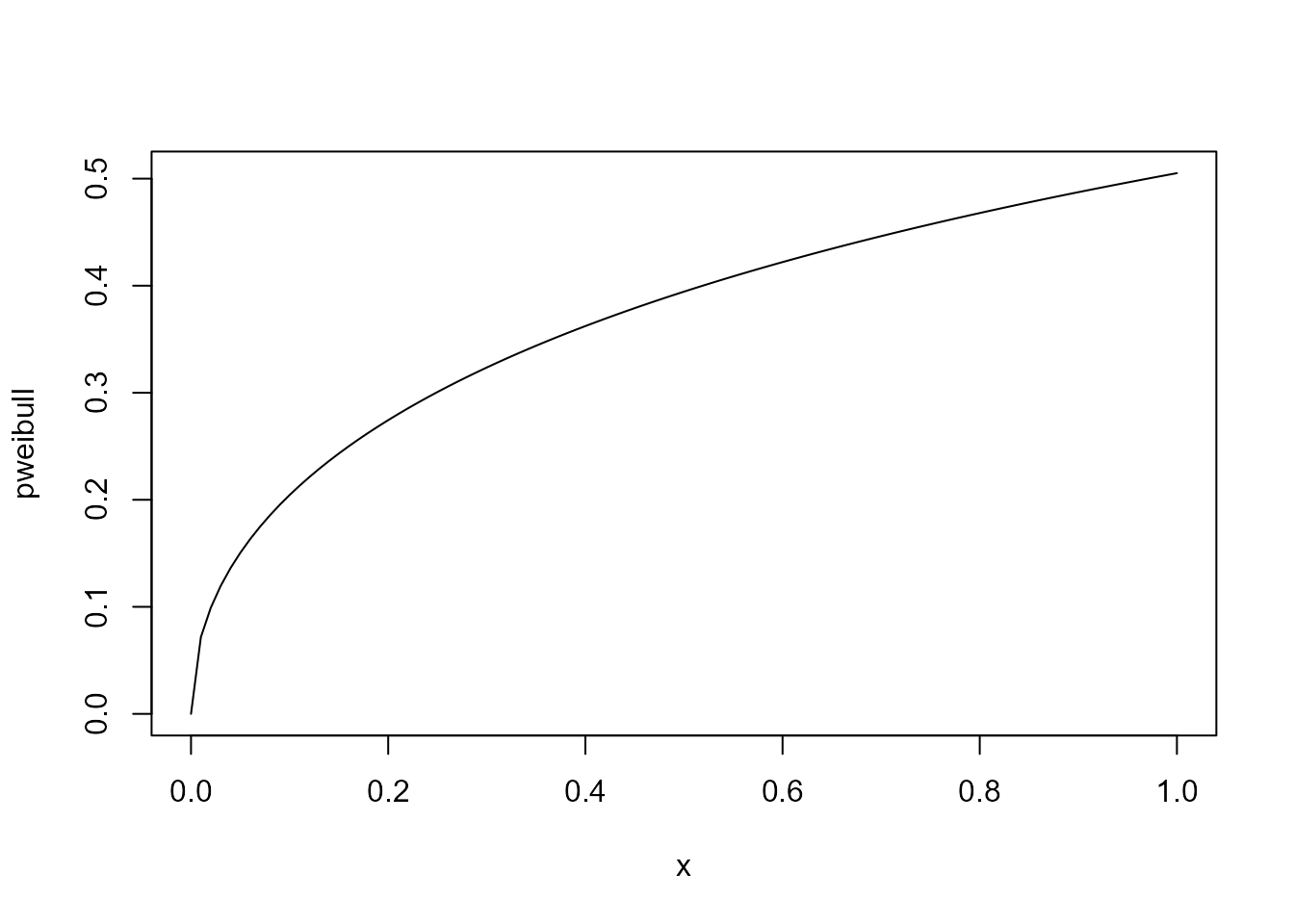

# quantile function
plot(fitted$qweibull,
     xlab = 'x',
     ylab = 'qweibull')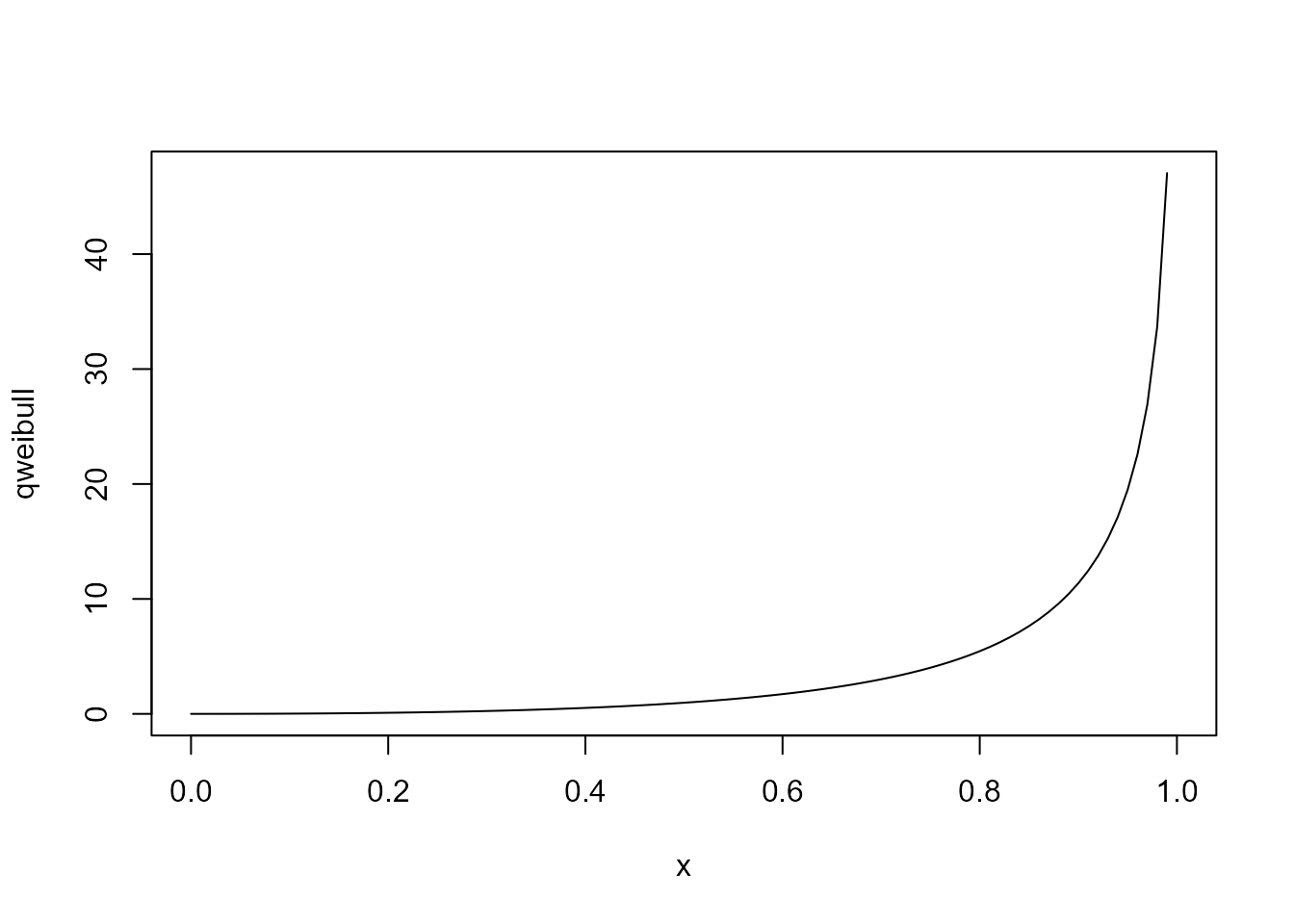

# sample from theoretical distribution
summary(fitted$rweibull(100))

##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
##  0.00001  0.18442  1.18814  4.83963  5.18201 81.99765

# estimated parameters from MLE
fitted$parameters

##     shape     scale 
## 0.4879054 2.0564428

Empirical Distributions

The package also allows users to specify empirical distributions. For discrete distributions, the function will not truncate any integer values with the given input. For continuous distributions, the function will create bins using the Freedman-Diaconis rule.

Discrete

set.seed(562)
x <- rpois(100, 5)
empDis <- fit_empirical(x)
# probability density function
plot(empDis$dempDis(0:10),
    xlab = 'x',
    ylab = 'dempDis')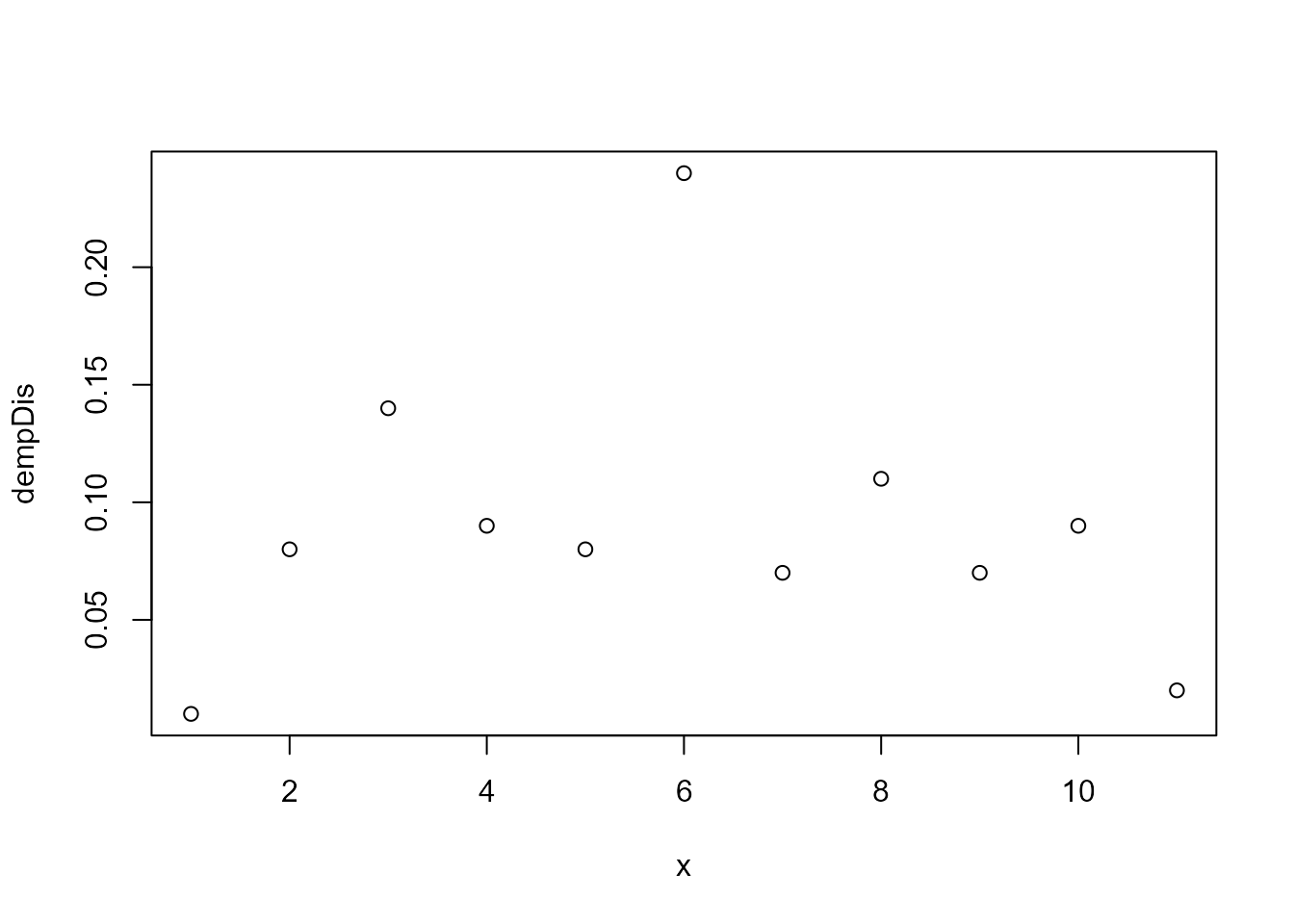

# cumulative distribution function
plot(x = 0:10,
    y = empDis$pempDis(0:10),
    #type = 'l',
    xlab = 'x',
    ylab = 'pempDis')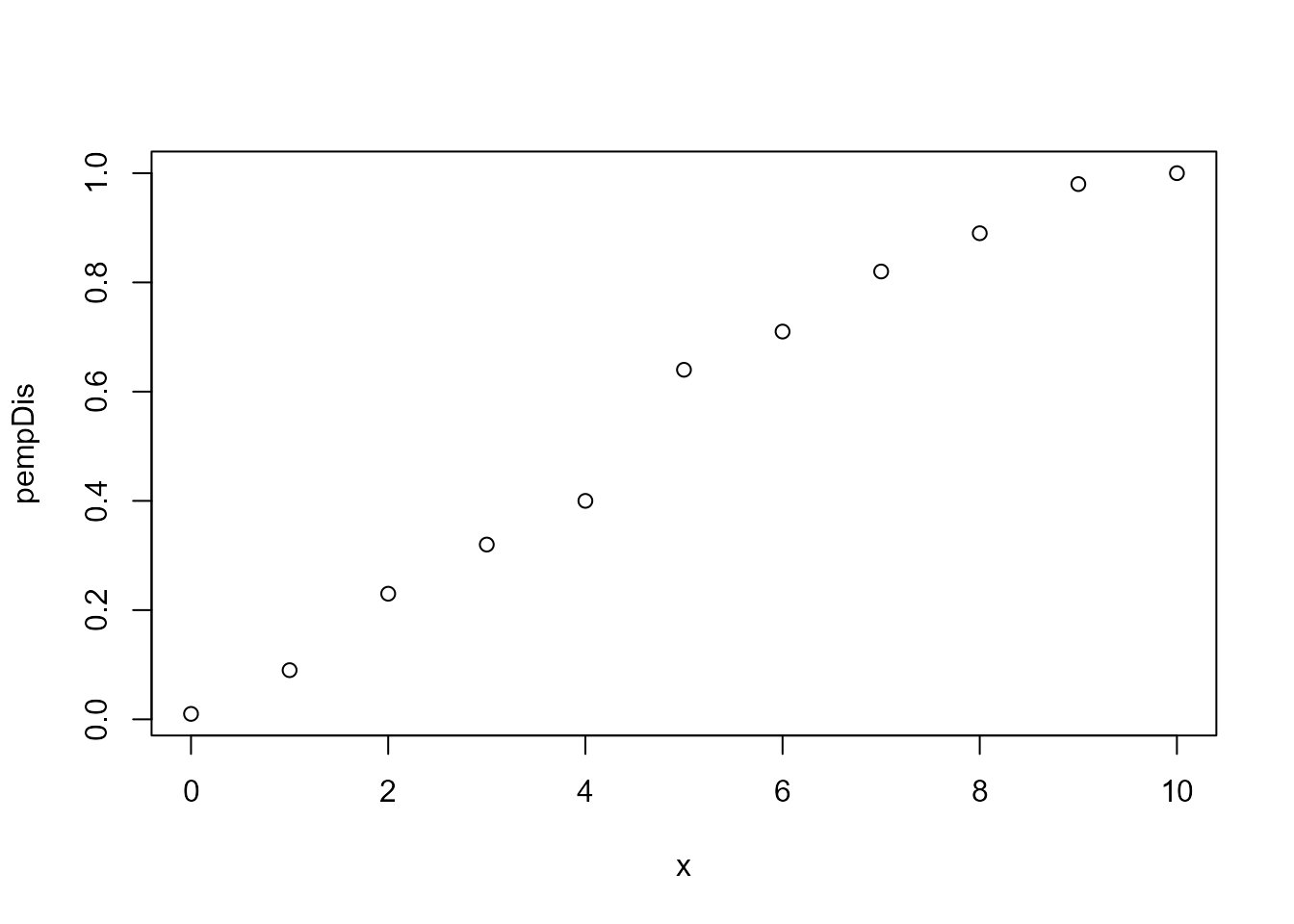

# quantile function
plot(x = seq(.1, 1, .1),
    y = empDis$qempDis(seq(.1, 1, .1)),
    type = 'p',
    xlab = 'x',
    ylab = 'qempDis')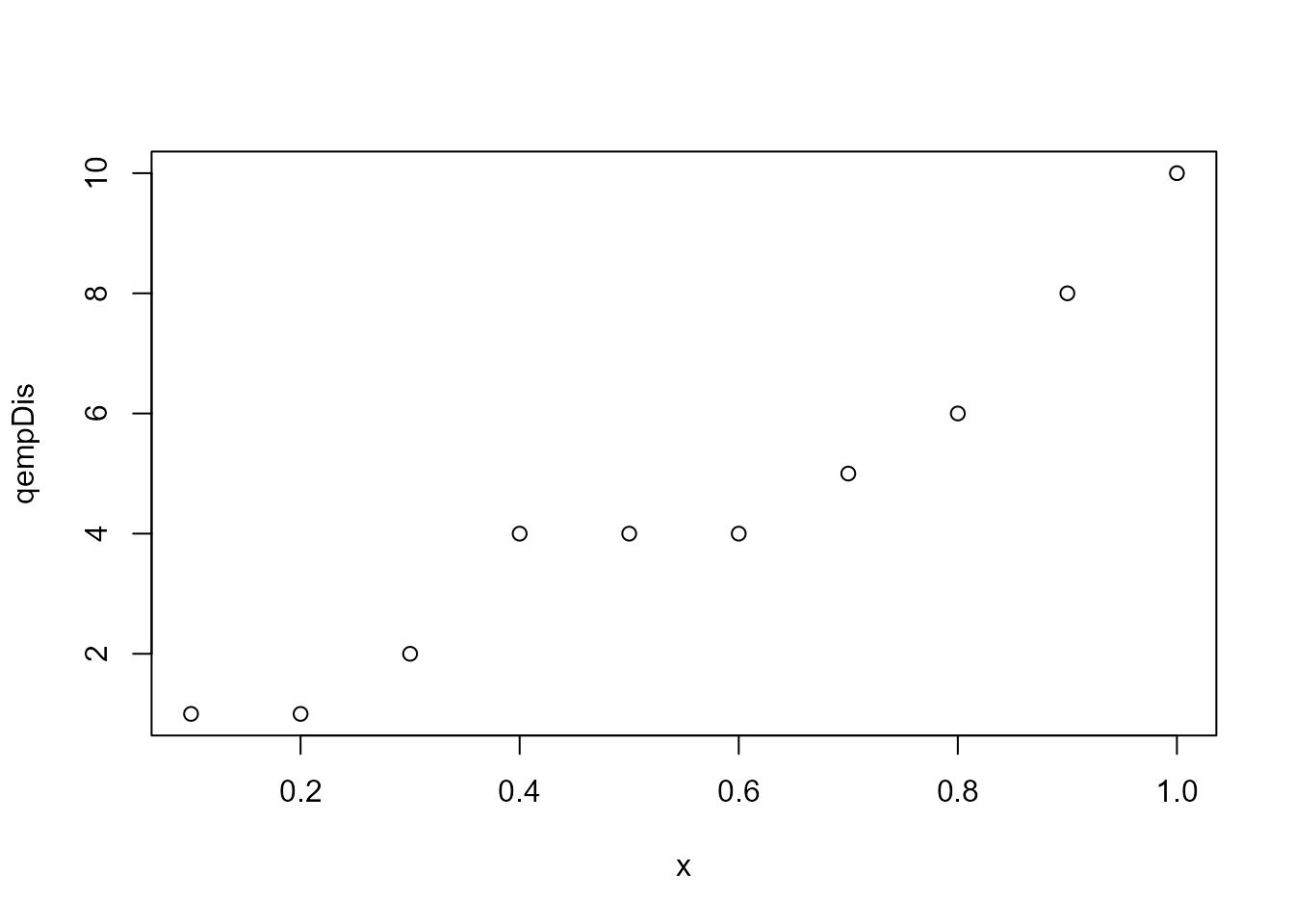

# random sample from fitted distribution
summary(empDis$r(100))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1.00    3.00    5.00    4.71    7.00   10.00

empDis$parameters

##    0    1    2    3    4    5    6    7    8    9   10 
## 0.01 0.08 0.14 0.09 0.08 0.24 0.07 0.11 0.07 0.09 0.02

Continuous

set.seed(562)
x <- rexp(100, 1/5)
empCont <- fit_empirical(x)
# probability density function
plot(x = 0:10,
     y = empCont$dempCont(0:10),
     xlab = 'x',
     ylab = 'dempCont')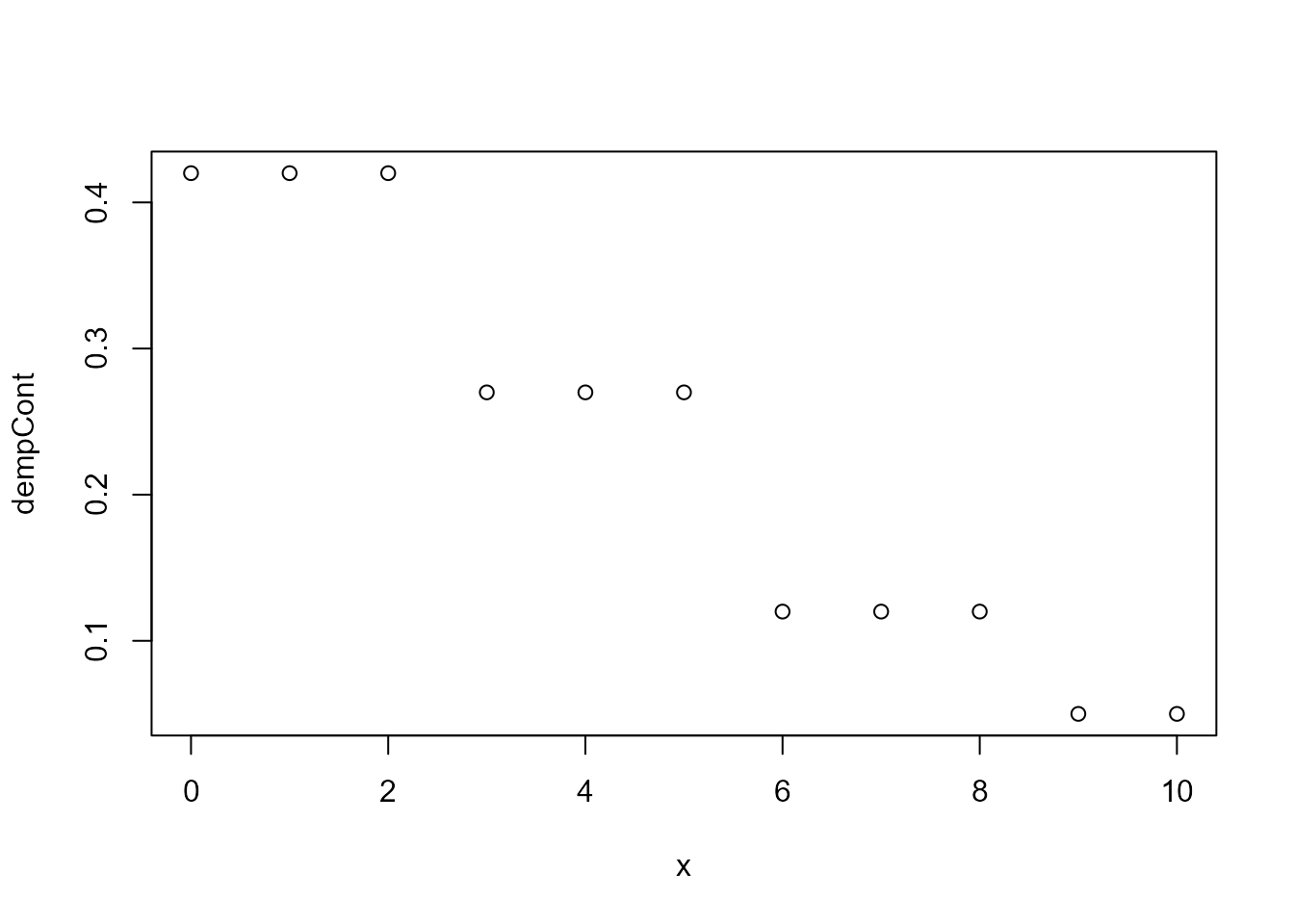

# cumulative distribution function
plot(x = 0:10,
     y = empCont$pempCont(0:10),
     #type = 'l',
     xlab = 'x',
     ylab = 'pempCont')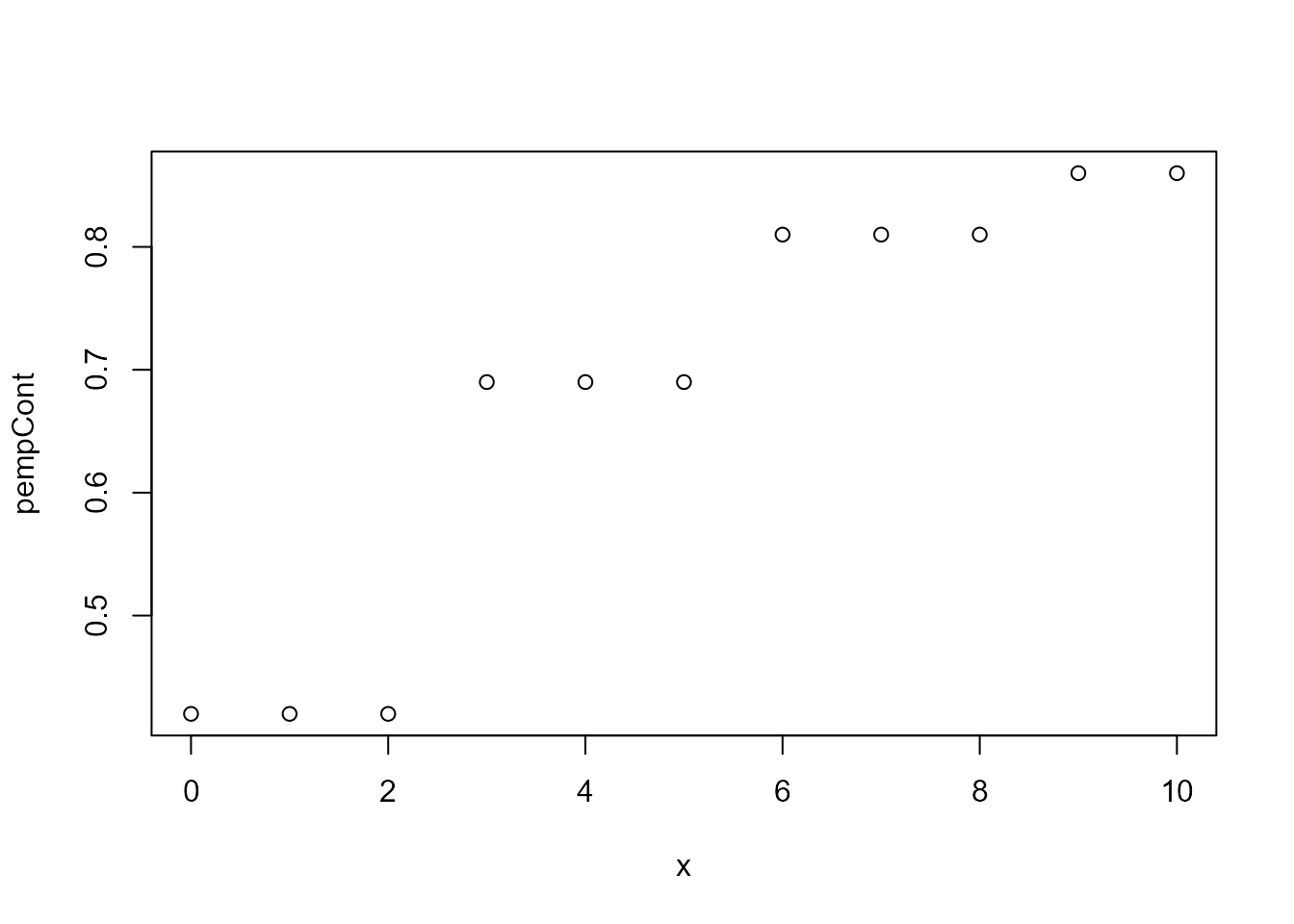

# quantile function
plot(x = seq(.1, 1, by = .1),
     y = empCont$qempCont(seq(.1, 1, by = .1)),
     type = 'p',
     xlab = 'x',
     ylab = 'qempCont')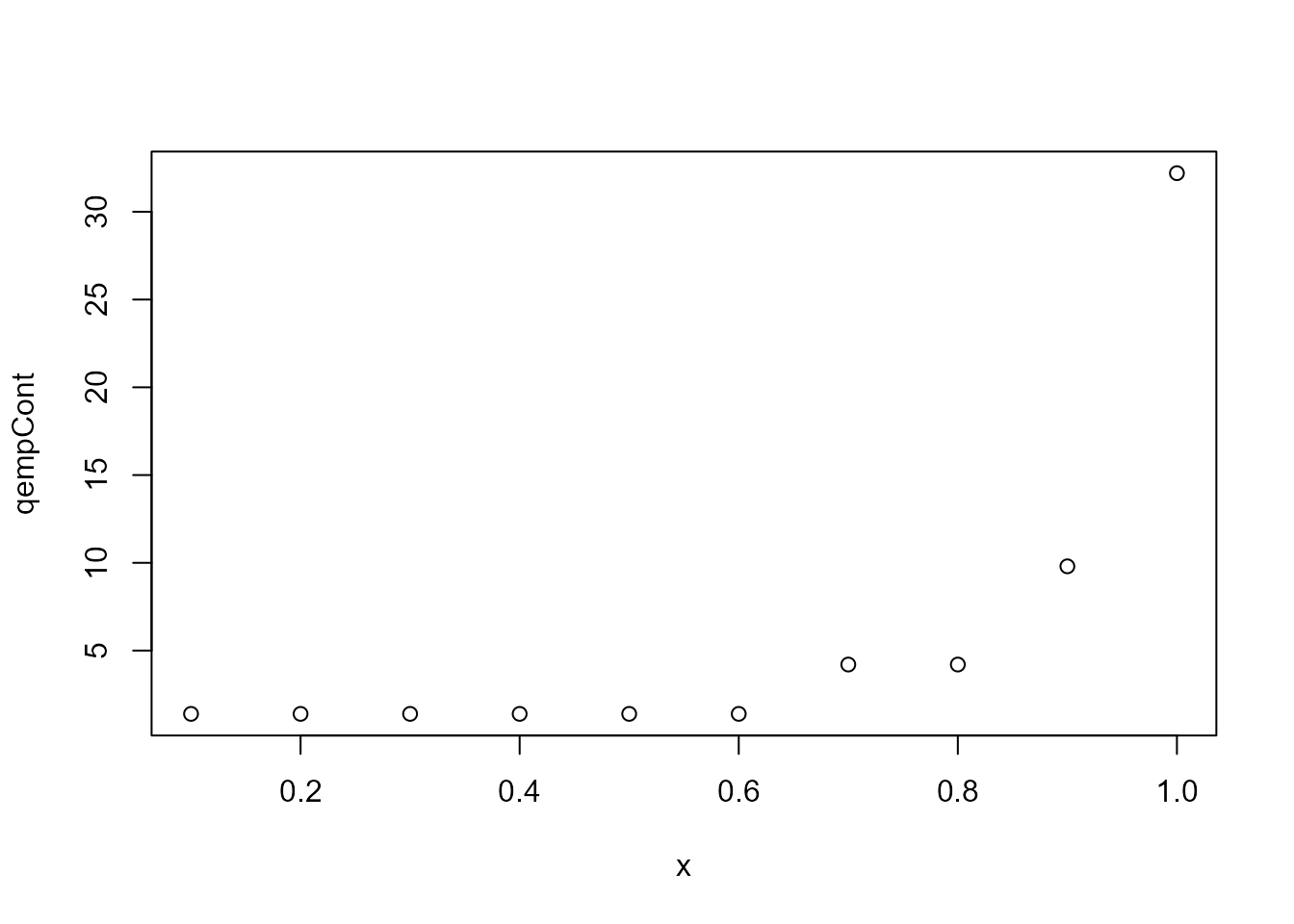

# random sample from fitted distribution
summary(empCont$r(100))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.394   1.394   4.205   4.871   4.205  32.200

empCont$parameters

## (-0.0217,2.81]     (2.81,5.6]      (5.6,8.4]     (8.4,11.2]      (11.2,14] 
##           0.42           0.27           0.12           0.05           0.06 
##      (14,16.8]    (16.8,19.6]    (19.6,22.4]    (22.4,25.2]      (25.2,28] 
##           0.01           0.04           0.01           0.01           0.00 
##      (28,30.8]    (30.8,33.6] 
##           0.00           0.01