Fit Empirical Distribution
fit_empirical(x)Arguments
- x
integer or double vector
Value
if integer vector then list of family functions for d, p, q, r, and parameters based on each integer value. if it is a double vector then list of family functions for d, p, q, r, and parameters based on Freedman-Diaconis rule for optimal number of histogram bins.
Examples
set.seed(562)
x <- rpois(100, 5)
empDis <- fit_empirical(x)
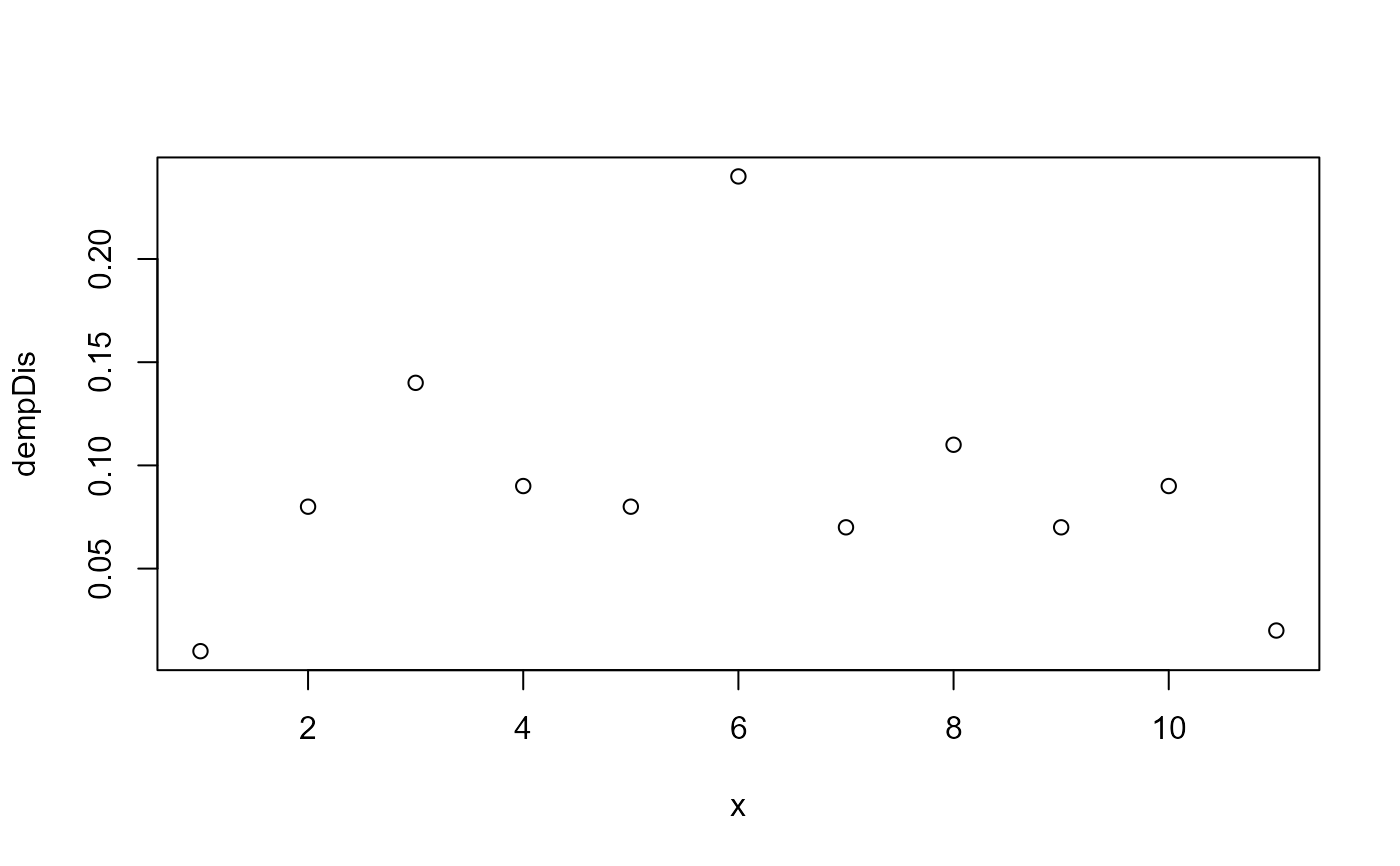
# probability density function
plot(empDis$dempDis(0:10),
xlab = 'x',
ylab = 'dempDis')
 # cumulative distribution function
plot(x = 0:10,
y = empDis$pempDis(0:10),
#type = 'l',
xlab = 'x',
ylab = 'pempDis')
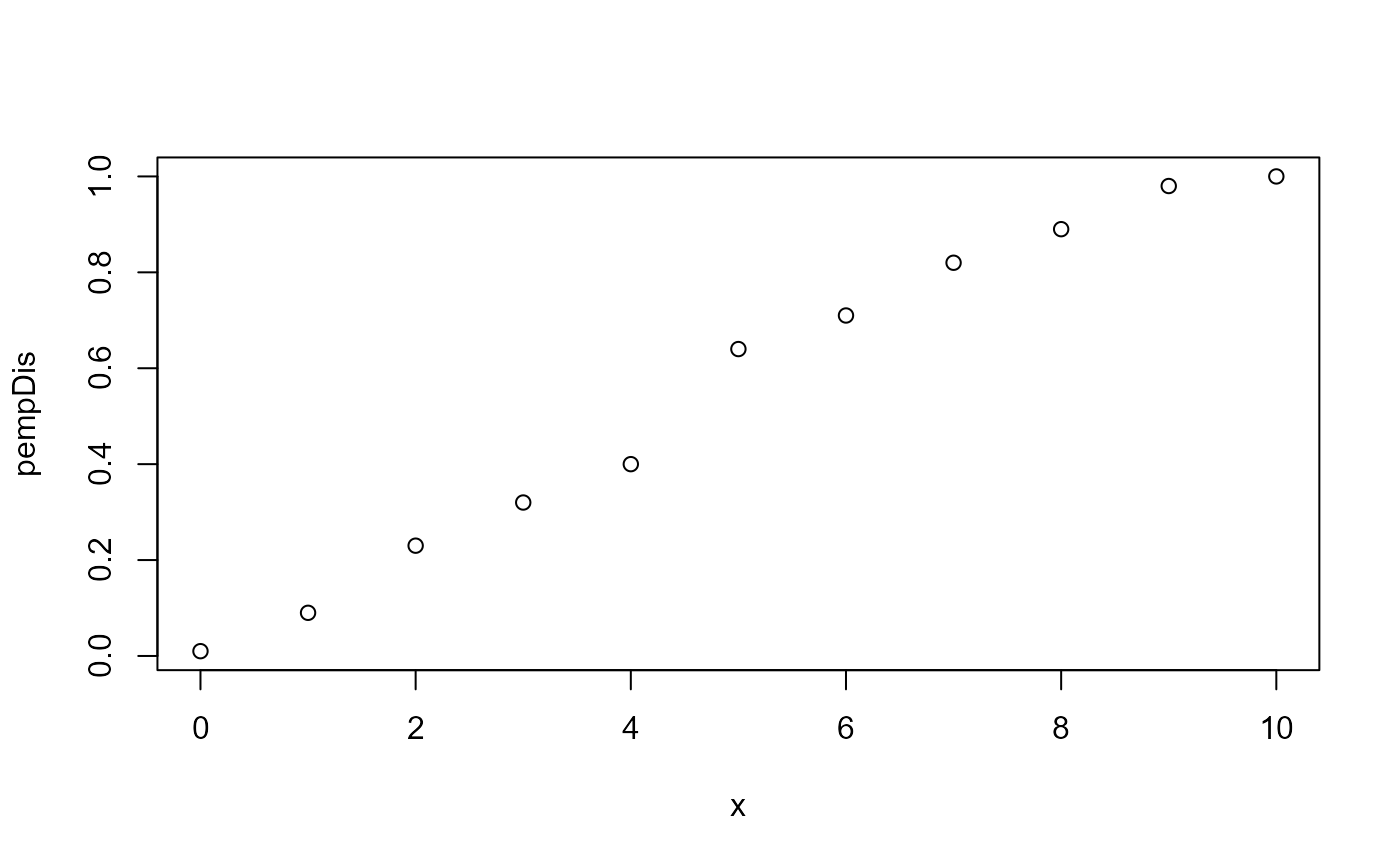
# cumulative distribution function
plot(x = 0:10,
y = empDis$pempDis(0:10),
#type = 'l',
xlab = 'x',
ylab = 'pempDis')
 # quantile function
plot(x = seq(.1, 1, .1),
y = empDis$qempDis(seq(.1, 1, .1)),
type = 'p',
xlab = 'x',
ylab = 'qempDis')
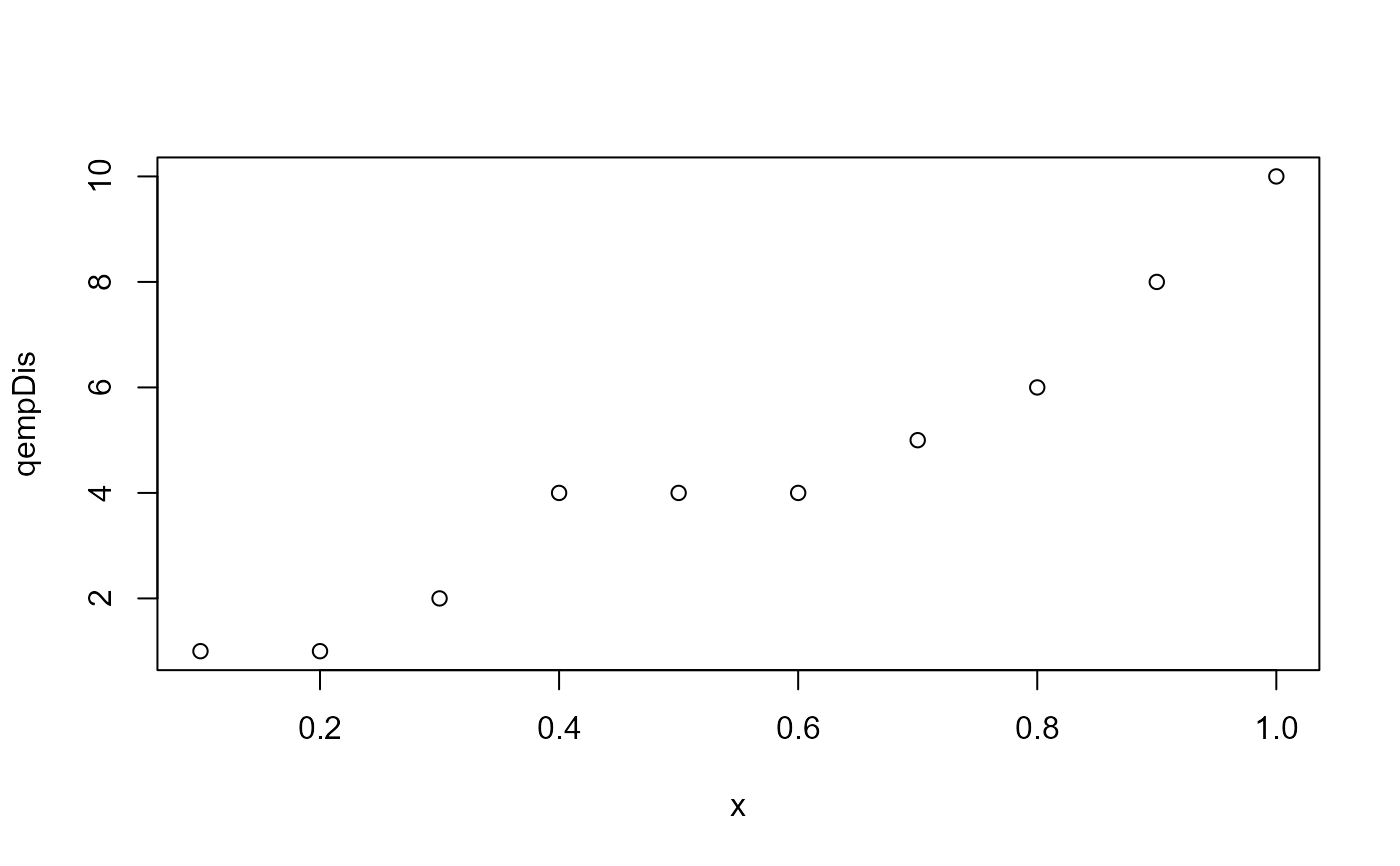
# quantile function
plot(x = seq(.1, 1, .1),
y = empDis$qempDis(seq(.1, 1, .1)),
type = 'p',
xlab = 'x',
ylab = 'qempDis')
 # random sample from fitted distribution
summary(empDis$r(100))
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.00 3.00 5.00 4.71 7.00 10.00
empDis$parameters
#> 0 1 2 3 4 5 6 7 8 9 10
#> 0.01 0.08 0.14 0.09 0.08 0.24 0.07 0.11 0.07 0.09 0.02
set.seed(562)
x <- rexp(100, 1/5)
empCont <- fit_empirical(x)
# probability density function
plot(x = 0:10,
y = empCont$dempCont(0:10),
xlab = 'x',
ylab = 'dempCont')
# random sample from fitted distribution
summary(empDis$r(100))
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.00 3.00 5.00 4.71 7.00 10.00
empDis$parameters
#> 0 1 2 3 4 5 6 7 8 9 10
#> 0.01 0.08 0.14 0.09 0.08 0.24 0.07 0.11 0.07 0.09 0.02
set.seed(562)
x <- rexp(100, 1/5)
empCont <- fit_empirical(x)
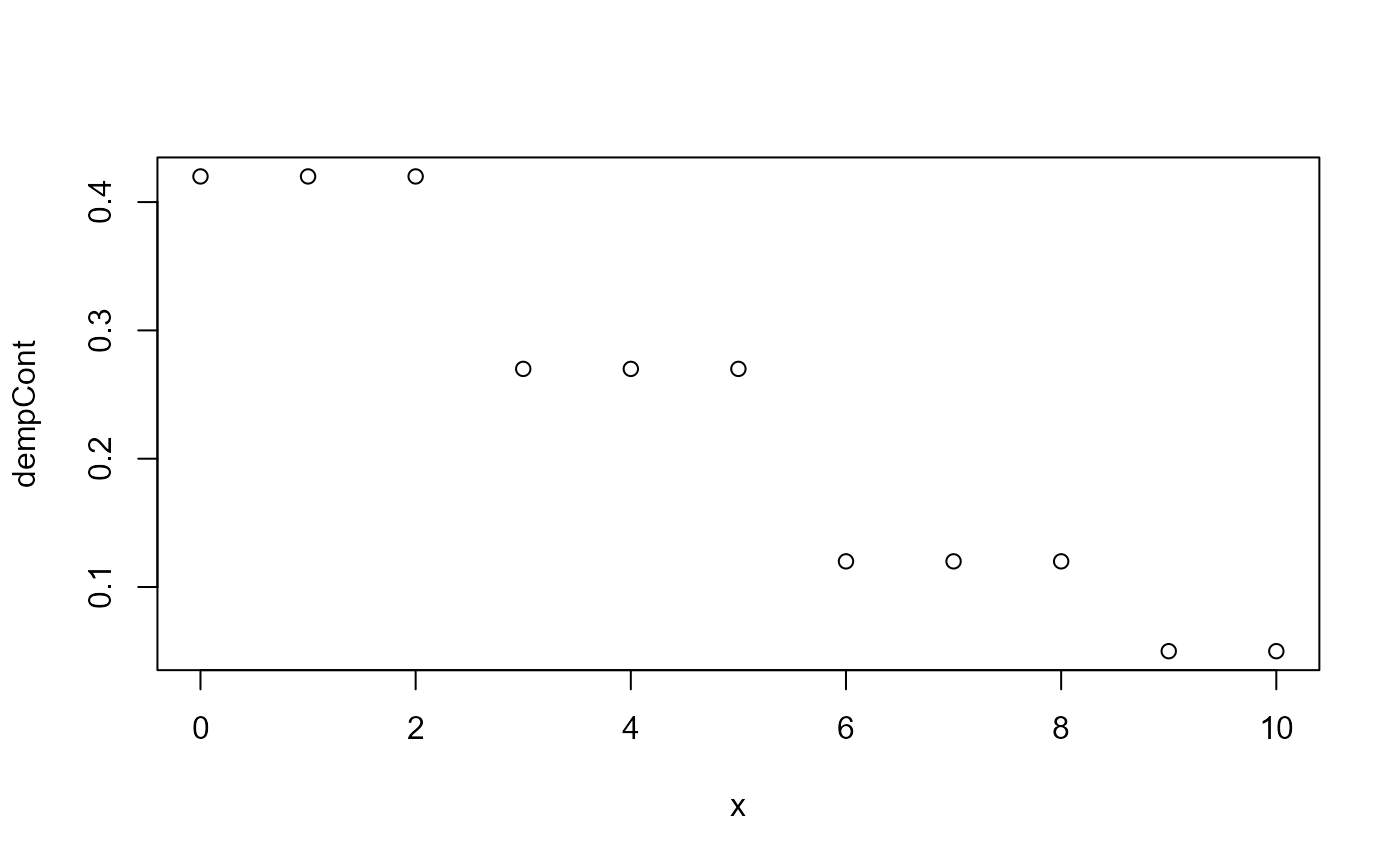
# probability density function
plot(x = 0:10,
y = empCont$dempCont(0:10),
xlab = 'x',
ylab = 'dempCont')
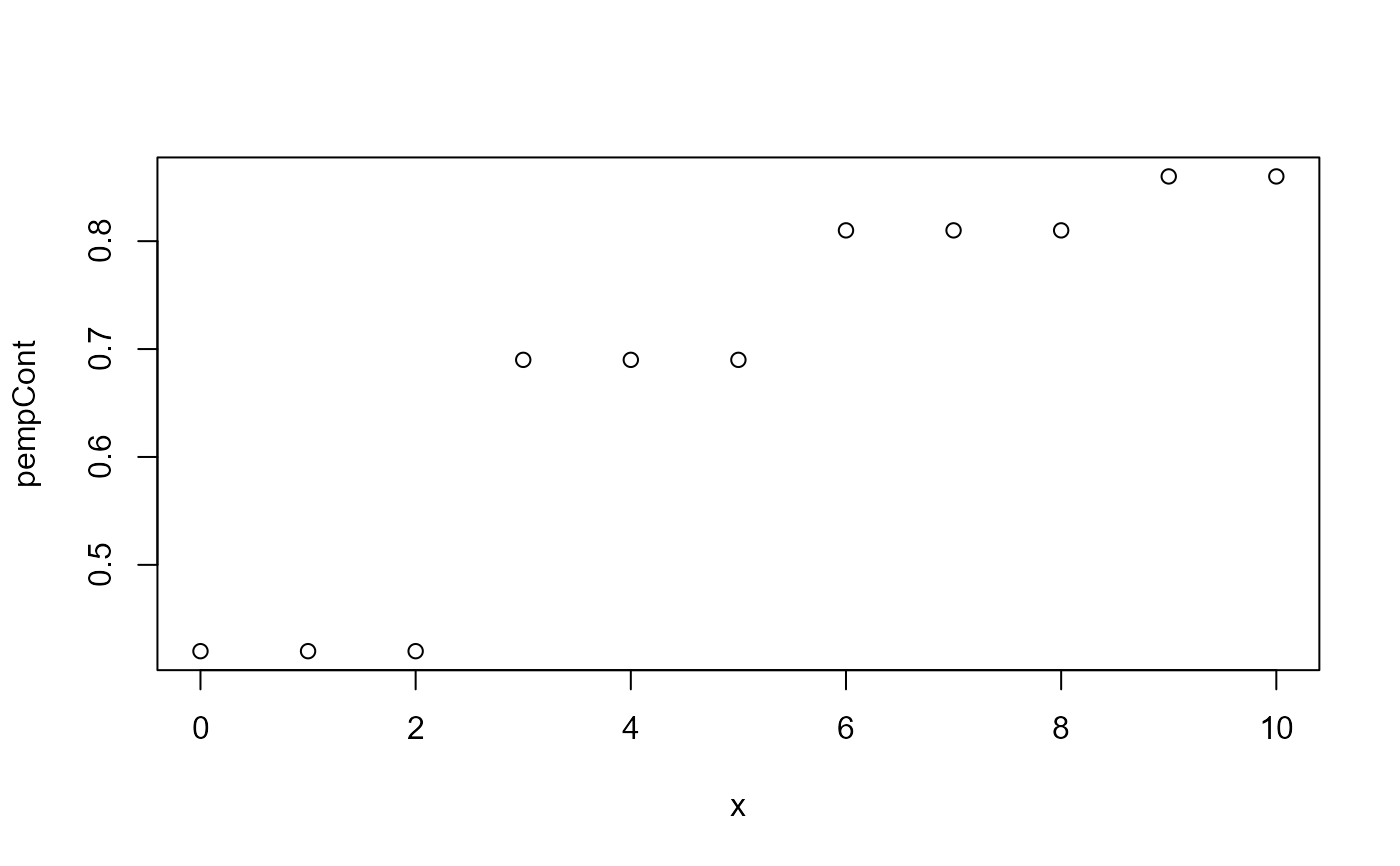
 # cumulative distribution function
plot(x = 0:10,
y = empCont$pempCont(0:10),
#type = 'l',
xlab = 'x',
ylab = 'pempCont')
# cumulative distribution function
plot(x = 0:10,
y = empCont$pempCont(0:10),
#type = 'l',
xlab = 'x',
ylab = 'pempCont')
 # quantile function
plot(x = seq(.5, 1, .1),
y = empCont$qempCont(seq(.5, 1, .1)),
type = 'p',
xlab = 'x',
ylab = 'qempCont')
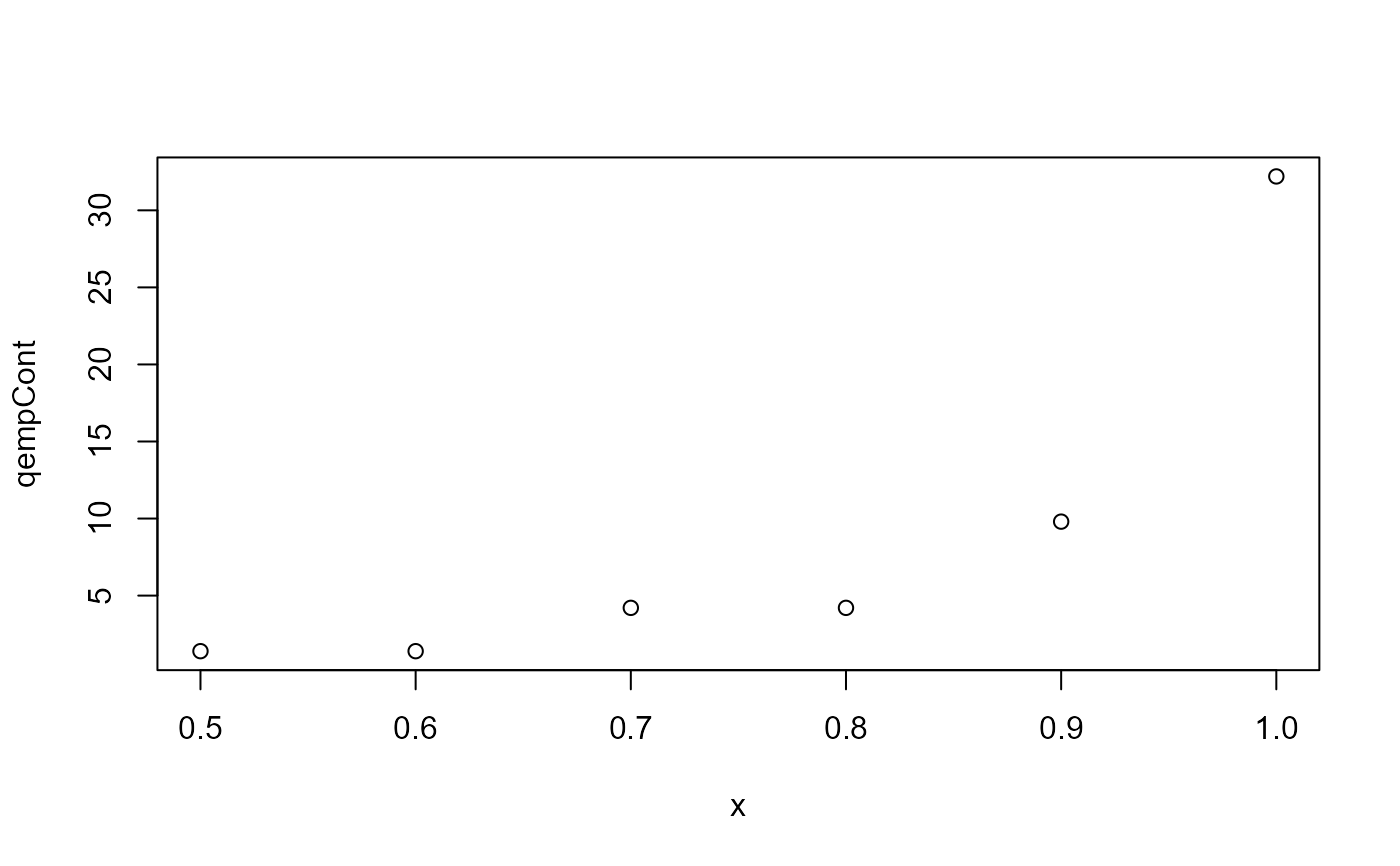
# quantile function
plot(x = seq(.5, 1, .1),
y = empCont$qempCont(seq(.5, 1, .1)),
type = 'p',
xlab = 'x',
ylab = 'qempCont')
 # random sample from fitted distribution
summary(empCont$r(100))
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.394 1.394 4.205 4.871 4.205 32.200
empCont$parameters
#> (-0.0217,2.81] (2.81,5.6] (5.6,8.4] (8.4,11.2] (11.2,14]
#> 0.42 0.27 0.12 0.05 0.06
#> (14,16.8] (16.8,19.6] (19.6,22.4] (22.4,25.2] (25.2,28]
#> 0.01 0.04 0.01 0.01 0.00
#> (28,30.8] (30.8,33.6]
#> 0.00 0.01
# random sample from fitted distribution
summary(empCont$r(100))
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 1.394 1.394 4.205 4.871 4.205 32.200
empCont$parameters
#> (-0.0217,2.81] (2.81,5.6] (5.6,8.4] (8.4,11.2] (11.2,14]
#> 0.42 0.27 0.12 0.05 0.06
#> (14,16.8] (16.8,19.6] (19.6,22.4] (22.4,25.2] (25.2,28]
#> 0.01 0.04 0.01 0.01 0.00
#> (28,30.8] (30.8,33.6]
#> 0.00 0.01